Why Do We even Need a Heatmap?

Modern 3D graphics still depends on the use of triangles, and quite a few of them at that.
These scenes tend to range from around 100,000 triangles at the low end, to more than
10,000,000 for a complex environment.
As soon as you exceed a few dozen triangles, brute-force (flat structure) ray-tracing becomes ever increasingly infeasible.

When ray-tracing you must test each ray against every triangle, and of those that actually intersect the ray, find the closest to the ray's origin. This operation has a complexity of O(N) with relation to triangle count. Even though each of these operations can be made quite efficient, doubling the complexity of the scene also doubles the rendering time.
While we could substantially decrease the rendering time by trying to optimize the intersection code, there’s an even better solution to this problem.

Acceleration structures -in my case a BVH (Bounding Volume Hierarchy), can be extremely effective at decreasing render time. Instead of storing the scene as a flat list of triangles, an acceleration structure (sometimes referred to as a ray accelerator) will break up the scene into smaller chunks. These are usually some kind of binary (or any other power of two) tree that divides the geometry by its location in space.

In the case of a BVH, our triangles will be sorted by one of the X/Y/Z planes, and then stored in a node. Each node contains indices to the first and last primitives it contains, and also the minimum and maximum of those primitives, forming an AABB (Axis-aligned Bounding Box).

Once the ray accelerator has built the tree for our scene, the renderer can then start casting rays. During ray traversal, the root node of the tree is tested, and if it intersects, will continue testing the branches below it. This continues until a leaf node is hit, and then the triangles contained within it will be tested.

By using this type of algorithmic optimization, the problem is reduced from O(N) to O(log2 N).
This prevents us from wasting potentially 10s of millions of primitive object tests, and instead takes us down to less than 100 for a well built tree.

Even though our algorithm should be substantially more efficient, we need a way to actually quantify its performance.

By adding accumulators we can easily keep count of: rays, primitives, and intersections.
Then after the render is completed, divide these totals by the time elapsed to get rays/second and primitives/second. Another metric useful for us is to divide the total number of primitives tested by the total rays cast. This gives us the average number of primitives-per-ray, which is a useful metric for determining tree quality.

In addition to that, we can simply visualize this quality by taking the number of primitives tested per ray (triangles/AABBs/planes/etc...) and using that to color each pixel.
This creates a heatmap estimating the "cost" of each pixel. Typically this is only performed by one
ray-cast per pixel, but it could also be extended to visualize the cost for path-tracing instead.

In my case I ended up just measuring a single ray-cast, and using HSV as the color conversion.
Worth noting is that I used the smoothStep function to interpolate the hue.
Linear mapping would be better for calibrated measurements, but really, just about any color mapping will work here, since we're just trying to get a rough feel of how well our algorithm is doing.

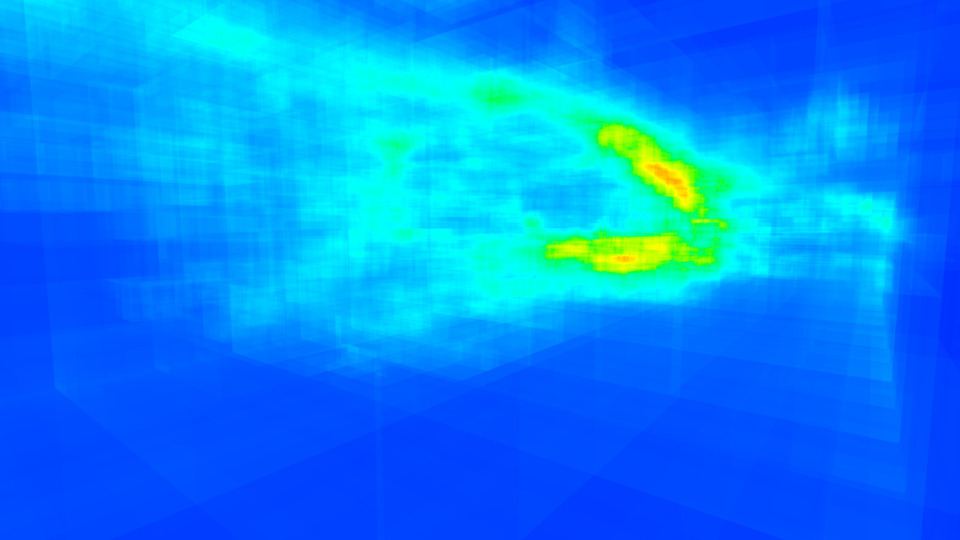
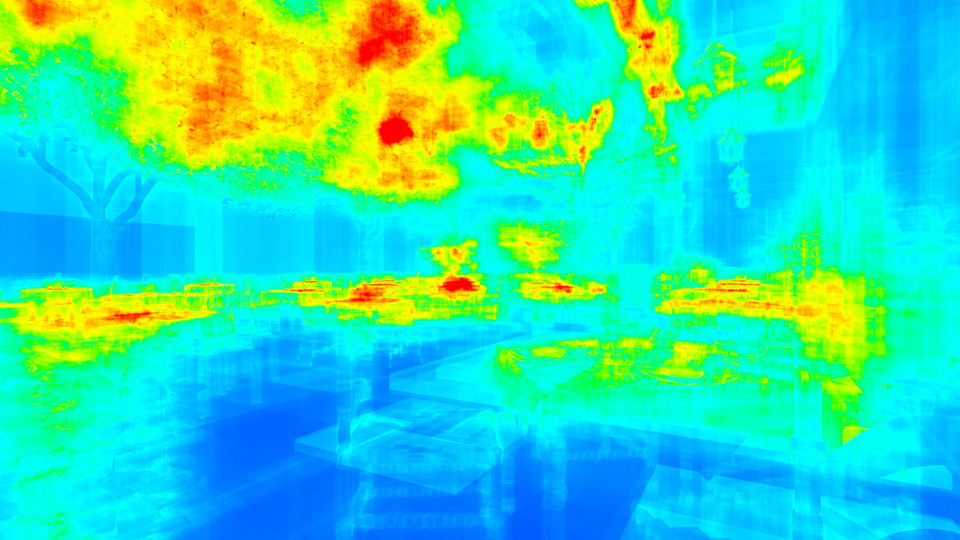Heatmaps of the ray-traversal cost for:
Cornell Box (Left), Lost Empire (Center), and San Miguel (Right).

For moderate scenes like my modified Cornell Box (887k triangles/324k nodes), the average cost is around 22 primitives per ray.
Then a more complex scene with regular geometry, like Lost Empire (225k triangles/113k nodes) tends to average around 160 primitives per ray. Its maximum is in the 6-700 range.
That's not bad, but not the best either.

However, complex scenes that have irregularly sized geometry, like the San-Miguel 2.0 model
(10M triangles/2.4M nodes) have by far the worst performance.
It's averaging around 390 primitive tests per ray. That's terrible! But what's even worse is the heatmap.
It shows that the maximum cost is more than 1,000 primitives per ray. What's going on?
Well my BVH algorithm is not capable of dealing with large overlapping triangles. That results in many nodes having lots of empty space, and overlapping each other.

In the future I'll experiment with creating a kd-tree (binary tree that divides space with planes), and adding Spatial-Splits to my BVH builder as well. Kd-trees tend to result in much better performance at the cost of increased build time and memory usage. However, using techniques like SBVH, promise to give the "best of both worlds" with regards to overall performance.

Copyright (c) 2021 David Williams